Probabilité : Cours-Résumés -Exercices-corrigés

Probabilité : Cours-Résumés -Exercices-corrigés

La théorie des probabilités fournit des modèles mathématiques permettant l’´étude d’expériences dont le résultat ne peut être prévu avec une totale certitude.

I- Expériences aléatoires et modèles

Le lancer d’une pièce de monnaie, le lancer d’un dé … sont des expériences aléatoires, car avant de les effectuer, on ne peut pas prévoir avec certitude quel en sera le résultat, résultat qui dépend en effet du hasard.

A cette expérience aléatoire, on associe l’ensemble des résultats possibles appelé univers. Ses éléments sont appelés éventualités.

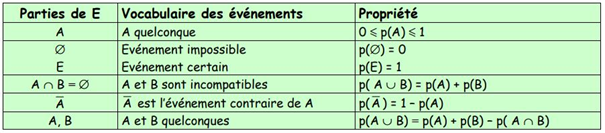
• Les sous-ensembles de l’univers Ω sont appelés événements.
• Les événements formés d’un seul élément sont appelés événements élémentaires.
• Etant donné un univers Ω, l’événement Ω est l’événement certain.
• L’ensemble vide est l’événement impossible.
• L’événement formé des éventualités qui sont dans A et dans B est noté A ∩ B et se lit A inter B.
• L’événement formé des éventualités qui sont dans A ou dans B est noté A ∪ B et se lit A union B.
• Etant donné un univers Ω et un événement A, l’ensemble des éventualités qui ne sont pas dans A constitue un événement appelé événement contraire de A, noté \bar { A }.
• A et B sont incompatibles si et seulement si A ∩ B = ∅.

Pour décrire mathématiquement une expérience aléatoire, on choisit un modèle de cette expérience ; pour cela on détermine l’univers et on associe à chaque événement élémentaire un nombre appelé probabilité.

II- Probabilités sur un ensemble fini

Soit Ω = {a1, a2, …, an} un ensemble fini. on définit une loi de probabilité sur Ω si on choisit des nombres p1, p2, …, pn tels que, pour  tout i, 0 ≤ pi ≤ 1 et p1 + p2 + … + pn = 1 ; pi est la probabilité élémentaire de l’événement {ai} et on note pi = p({ai}) ou parfois plus simplement p(ai).

Propriétés

Equiprobabilité

On dit qu’il y a équiprobabilité quand tous les événements élémentaires ont la même probabilité.

Calculs dans le cas d’équiprobabilité

Dans une situation d’équiprobabilité, si Ω a n éléments et si E est un événement composé de m événements élémentaires : p(E)=\frac { Card\quad E }{ Card\quad \Omega } où card E et card Ω désignent respectivement le nombre d’éléments de E et de Ω. On le mémorise souvent en disant que c’est le nombre de cas favorables divisé par le nombre de cas possibles.

III- Variables aléatoires

Une variable aléatoire X est une application définie sur un ensemble E muni d’une probabilité P, à valeurs dans R.

• X prend les valeurs x1, x2, …, xn avec les probabilités p1, p2, …, pn définies par : pi = p(X = xi).
• L’affectation des pi aux xi permet de définir une nouvelle loi de probabilité. Cette loi notée PX, est appelée loi de probabilité de X.

Soit X une variable aléatoire prenant les valeurs x1, x2, …, xn avec les probabilités p1, p2, …, pn. On appelle respectivement espérance mathématique de X, variance de X et écart-type de X , les nombres suivants :

• l’espérance mathématique est le nombre E(X) défini par : E(X)\sum { i=1 }^{ n }{ ({ p }{ i }{ x }_{ i } } )
• la variance est le nombre V défini par : V(X)=\sum{ i=1 }^{ n }{ { p }{ i }{ ({ x }{ i }-E(X)) }^{ 2 } } =\sum{ i=1 }^{ n }{ { p }{ i }{ { { x }{ i } }^{ 2 }-E(X) }^{ 2 } }
• l’écart – type est le nombre σ défini par : \sigma =\sqrt { V }

IV- Conditionnement

Arbres pondérés

• La somme des probabilités des branches issues d’un même nœud est 1.
• La probabilité de l’événement correspondant à un trajet est le produit des probabilités des différentes branches composant ce trajet.

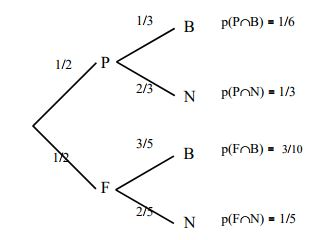
 Exemple

On jette une pièce.

• Si on obtient pile, on tire une boule dans l’urne P contenant 1 boule blanche et 2 boules noires.
• Si on obtient face, on tire une boule dans l’urne F contenant 3 boules blanches et 2 boules noires.

On peut représenter cette expérience par l’arbre pondéré ci-dessous :

Probabilité conditionnelle

p désigne une probabilité sur un univers fini Ω. A et B étant deux événements de Ω, B étant de probabilité non nulle.

• On appelle probabilité conditionnelle de l’événement A sachant que B est réalisé le réel noté : p(A/B)=\frac { p(A\bigcap { B) } }{ p(A) }
• Le réel p(A /B) se note aussi { p }_{ B }(A) et se lit aussi probabilité de A sachant B

Si A et B sont tous deux de probabilité non nulle, alors les probabilités conditionnelles p(A/B) et p(B/A) sont toutes les deux définies et on a : p(A ∩ B) = p(A/B)p(B) = p(B/A)p(A).

V- Indépendance

 a. Événements indépendants

 A et B sont 2 événements de probabilité non nulle.

• A et B sont indépendants lorsque la réalisation de l’un ne change pas la réalisation de l’autre.
• A et B sont indépendants si et seulement si p(A/B) = p(A) ou p(B/A) = p(A).

Deux événements A et B de probabilité non nulle sont indépendants si et seulement si ils vérifient une des trois conditions :  p(A/B) = p(A) ou p(B/A) = p(B) ou p( A ∩ B) = p(A)p(B).

 b. Indépendance de deux variables aléatoires

X et Y sont deux variables définies sur l’univers Ω d’une expérience aléatoire ; X prend les valeurs x1, x2, …, xn et Y prend les valeurs y1, y2, …, yq. Définir la loi du couple (X, Y) c’est donner la probabilité pi,j de chaque événement  [(X = xi) et (Y = yj)].

c. Probabilités totales

Soient Ω un univers associé à une expérience aléatoire et n un entier ≥ 2. Les événements A1, A2, …, An forment une partition de Ω si les trois conditions suivantes sont réalisées :

• Pour tout i ∈ {1 ; 2 ;… ; n}, Ai ≠ 0.
• Pour tous i et j (avec i ≠ j) de {1 ;2 ;…n}, Ai ∩ Aj ≠ ∅.
• A1 ∪ A2 ∪ … ∪ An = E.

Formule des probabilités totales

Soient A1, A2, …, An une partition de l’univers Ω constituée d’événements de probabilités non nulles et B un événement quelconque contenu dans Ω. Alors :

• p(B) = p(B ∩ A1) + p(B ∩ A2) + … + p(B ∩ An) 
• Ou p(B)={ p }{ A1 }(B)\times { p }(A1)+{ p }{ A2 }(B)\times { p }(A2)+KK+{ p }_{ An }(B)\times { p }(An)

VI- Lois de probabilité

 Loi de Bernoulli

Une alternative est une épreuve à deux issues possibles :

• Le succès, noté 1, de probabilité p,
• L’échec, noté 0, de probabilité q = 1 – p.

Sa loi de probabilité est appelée loi de Bernoulli de paramètre p.

 Exemple

Un dé cubique est mal équilibré : la probabilité d’obtenir 6 est de 1/7.

On appelle succès l’événement « obtenir 6 » et échec « obtenir un numéro différent de 6 ».

Cette expérience qui ne comporte que deux issues suit une loi de Bernoulli. Si On effectue cinq fois cette expérience. On est en présence d’un schéma de Bernoulli.

Théorème

Pour une loi de Bernoulli de paramètre p, l’espérance est p et l’écart type est \sqrt { pq }

 Loi Binomiale

Soit un schéma de Bernoulli constitué d’une suite de n épreuves. Soit X la variable aléatoire égale au nombre de succès obtenus, alors :

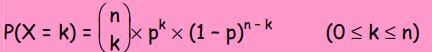
Théorème

Pour une loi Binomiale de paramètres n et p, l’espérance est np et l’écart type est n \sqrt { npq }

Exemple

Dans l’exemple précédent, on appelle X la variable aléatoire comptant le nombre de succès à l’issue des 5 lancés. On obtient les probabilités suivantes :

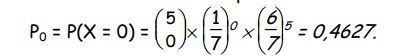
P1 =0,3856 ; P2 = 0,1285 ; P3 = 0,0214 ; P4 = 0,0018 ; P5 = 0,0001

Pour plus de détails télécharger les documents ci-dessous:

---

Liens de téléchargement des cours de Probabilité

---

Liens de téléchargement des résumés de Probabilité

---

Liens de téléchargement des exercices corrigés de Probabilité

---

Voir aussi :

---

Partagez au maximum pour que tout le monde puisse en profiter

---