Théorème de Pythagore-Cours et Exercices corrigés

Théorème de Pythagore-Cours et Exercices corrigés

I- Théorème de Pythagore

Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.

1- Enoncé du théorème de Pythagore

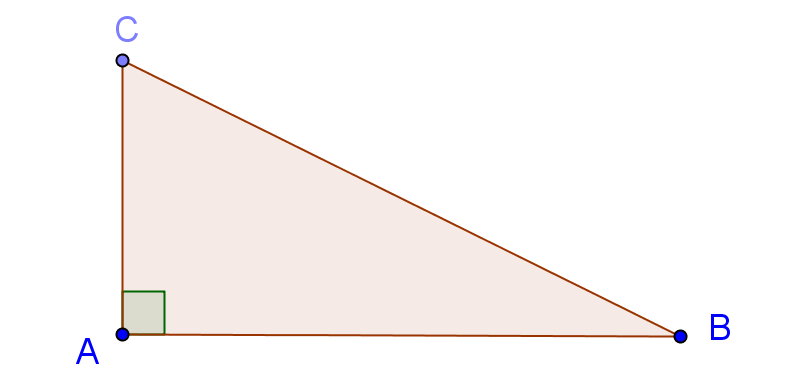
Si ABC est un triangle rectangle en A alors :

BC² = AB² + AC²

• Avec l’hypoténuse est côté le plus long dans un triangle rectangle : c’est le côté où il n’y a pas d’angle droit.

Le théorème de Pythagore dit plusieurs choses importantes :

• Le théorème ne s’applique que sur le triangle rectangle.
• Le théorème permet de calculer les côtés du triangle rectangle.
• Pour appliquer le théorème, il faut connaître la valeur de 2 côtés pour pouvoir calculer la valeur du 3ème.

2- Exemples d’utilisation du théorème de Pythagore

On connaît 2 côtés du triangle rectangle, il permet de calculer la longueur du troisième côté.

a- Exemple 1 :

• Le triangle ALI est rectangle en A.
• Son hypoténuse est [IL].
• L’énoncé de Pythagore permet d’écrire : IL² = AI² + AL²
• D’après les données, on a: AI=12 et AL=9
• donc IL2 = 144+81= 225
• donc IL=15 cm

b- Exemple 2 :

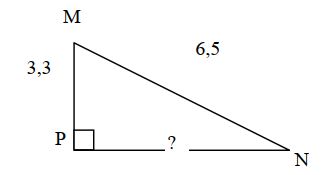
• Le  triangle  MNP  est  rectangle  en  P. Son  hypoténuse  est  [MN].
•  L’énoncé  de  Pythagore  permet  d’écrire : MN2  =  MP2  +  PN2
• D’après  les  données,  on  a: MN=6,5  et  MP=3,3
• Donc 6,5² = 3,3²+PN² ==> 42,25=10,89+PN²
• On a PN² = 42,25‐10,89 = 31,36
• Donc PN = 5,6 cm

II- La réciproque du théorème de Pythagore

Si dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, alors ce triangle est rectangle.

1- Enoncé de la réciproque du théorème de Pythagore

2- Méthode : Savoir si un triangle est rectangle ou non.

On donne les longueurs des 3 côtés d’un triangle ABC, le triangle est-il rectangle ?

• On repère le côté le plus long et on calcule le carré de sa longueur.
• On calcule la somme des carrés des longueurs des deux autres côtés.
• S’il y a égalité, la réciproque permet d’affirmer que le triangle est rectangle. S’il y a inégalité, le triangle n’est pas rectangle.

3- Exemples

Les triangles suivants sont-ils rectangles ?

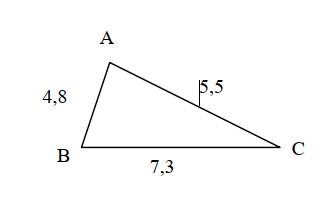
Exemple 1 :

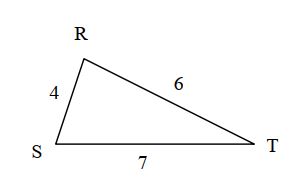
Exemple 2 :

Pour plus de détails télécharger les documents ci-dessous:

---

Liens de téléchargement des cours sur le Théorème de Pythagore

---

Liens de téléchargement des exercices corrigés sur le Théorème de Pythagore

---

Voir aussi :

---

Partagez au maximum pour que tout le monde puisse en profiter

---