
Produit scalaire : Cours-Résumés-Exercices corrigés
I- Définitions
I-1- Définition initiale
On appelle produit scalaire de deux vecteurs \vec { u } et\quad \vec { v } , le nombre réel noté \vec { u } .\vec { v } tel que :
\vec { u } .\vec { v } =\frac { 1 }{ 2 } ({ \left| \vec { u } +\vec { v } \right| }^{ 2 }-{ \left| \vec { u } \right| }^{ 2 }-{ \left| \vec { v } \right| }^{ 2 })
Exemple :
Calculer le produit scalaire \vec { AB } .\vec { AD } pour la figure suivante :
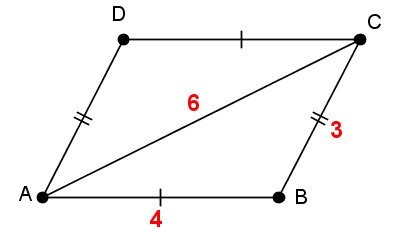
Comme ABCD est un parallélogramme, on a \vec { AB } +\vec { AD } =\vec { AC } donc :
\vec { AB } .\vec { AD } =\frac { 1 }{ 2 } ({ \vec { AC } }^{ 2 }-{ \vec { AB } }^{ 2 }-{ \vec { AD } }^{ 2 })
\vec { AB } .\vec { AD } =\frac { 1 }{ 2 } ({ AC }^{ 2 }-{ AB }^{ 2 }-{ AD }^{ 2 })
\vec { AB } .\vec { AD } =\frac { 1 }{ 2 } (36-16-9)
\vec { AB } .\vec { AD } =\frac { 11 }{ 2 }
I-2- Définition dans un repère orthonormal
Dans un repère orthonormal (O,\vec { i } ,\vec { j } ) le produit scalaire de deux vecteurs \vec { u } et\vec { v } de coordonnées respectives (x;y)\quad et\quad (x\prime ;y\prime ) est égal à :
\vec { u } .\vec { v } =\quad xx\prime +yy\prime
On peut aussi utiliser la notation matricielle :
(\begin{matrix} x \ y \end{matrix}).(\begin{matrix} x\prime \ y\prime \end{matrix})=\quad xx\prime +yy\prime
Démonstration
Montrons que cette définition est équivalente à la définition initiale
On rappelle que si un vecteur \vec { u } a pour coordonnées (x; y) alors :
{ \left| \vec { u } \right| }^{ 2 }={ \quad x }^{ 2 }+{ y }^{ 2 }
On a alors :
\vec { u } .\vec { v } =\frac { 1 }{ 2 } ({ \left| \vec { u } +\vec { v } \right| }^{ 2 }-{ \left| \vec { u } \right| }^{ 2 }-{ \left| \vec { v } \right| }^{ 2 })
\vec { u } .\vec { v } =\frac { 1 }{ 2 } \left[ { (x+x\prime ) }^{ 2 }+{ (y+y\prime ) }^{ 2 }-({ x }^{ 2 }+{ y }^{ 2 })-({ x\prime }^{ 2 }+{ y\prime }^{ 2 }) \right]
\vec { u } .\vec { v } =\frac { 1 }{ 2 } \left[ 2xx\prime +2yy\prime \right]
\vec { u } .\vec { v } =\quad xx\prime +yy\prime
Exemple :
Déterminer le produit scalaire :
\vec { AB } .\vec { AC }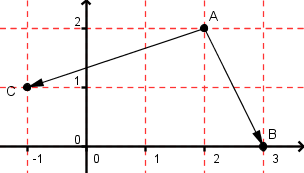
\vec { AB } .\vec { AC } =\begin{pmatrix} 3 & -2 \ 0 & -2 \end{pmatrix}.\begin{pmatrix} -1 & -2 \ 1 & -2 \end{pmatrix}
\vec { AB } .\vec { AC } =\left( \begin{matrix} 1 \ -2 \end{matrix} \right) .\left( \begin{matrix} -3 \ -1 \end{matrix} \right)
\vec { AB } .\vec { AC } =\quad 1\times (-3)+(-2)\times (-1)
\vec { AB } .\vec { AC } =\quad -1
I-3- Définition projective
Le produit scalaire de deux vecteurs \vec { u } et\vec { v } est défini par :
\vec { u } .\vec { v } =\quad \left| \vec { u } \right| \times \left| \vec { v } \right| \times \cos { (\vec { u } ,\vec { v } ) }
Exemple
Déterminer le produit scalaire :
\vec { AB } .\vec { AC }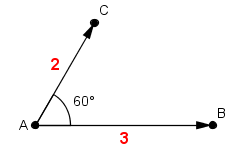
\vec { AB } .\vec { AC } =\quad \left| \vec { AB } \right| \times \left| \vec { AC } \right| \times \cos { ({ 60 }^{ \circ }) }
\vec { AB } .\vec { AC } =\quad AB\times AC\times \cos { ({ 60 }^{ \circ }) }
\vec { AB } .\vec { AC } =\quad 3\times 2\times \frac { 1 }{ 2 }
\vec { AB } .\vec { AC } =\quad 3
II- Propriétés
Propriété 1
1- Le produit scalaire est commutatif : \vec { u } .\vec { v } =\quad \vec { v } .\vec { u }
2- Le produit scalaire est distributif par rapport à l’addition de deux vecteurs :\vec { u } .(\vec { v } +\vec { w } )=\quad \vec { u } .\vec { v } +\vec { u } .\vec { w }
3- Le produit scalaire est distributif par rapport à la multiplication par un
scalaire : (a\vec { u } )+(b\vec { v } )=\quad ab\times (\vec { u } .\vec { v } )
4- Si les vecteurs \vec { u } et\vec { v } sont colinéaires et de même sens alors : \vec { u } .\vec { v } =\left| \vec { u } \right| \times \left| \vec { v } \right|
5- Si les vecteurs \vec { u } et\vec { v } sont colinéaires et de sens contraires alors :\vec { u } .\vec { v } =-\left| \vec { u } \right| \times \left| \vec { v } \right|
6 Si les vecteurs \vec { u } et\vec { v } sont perpendiculaires alors : \vec { u } .\vec { v } =\quad 0
III- Projection
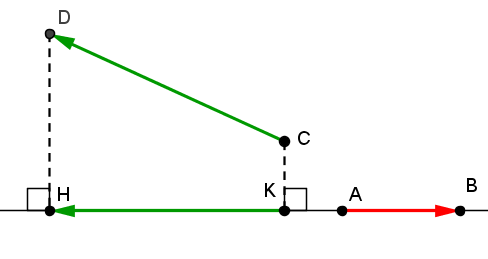
Soit deux vecteurs \vec { AB } et\vec { CD } . On appelle K et H les projections orthogonales respectives de C et D sur la droite AB, on a alors :
si \vec { AB } et\vec { KH } sont de même sens
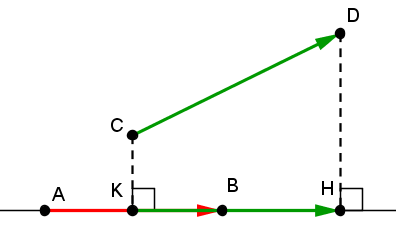
si \vec { AB } et\vec { KH } sont de sens contraires
Pour plus de détails télécharger les documents ci-dessous:
Liens de téléchargement des cours sur le Produit scalaire
Cours sur le Produit scalaire N°1
Cours sur le Produit scalaire N°2
Cours sur le Produit scalaire N°3
Cours sur le Produit scalaire N°4
Cours sur le Produit scalaire N°5
Liens de téléchargement des résumés sur le Produit scalaire
Résumé surl e Produit scalaire N°1
Résumé sur le Produit scalaire N°2
Résumé sur le Produit scalaire N°3
Liens de téléchargement des exercices corrigés sur le Produit scalaire
Exercices corrigés sur le Produit scalaire N°1
Exercices corrigés sur le Produit scalaire N°2
Exercices corrigés sur le Produit scalaire N°3
Le groupe m’intéresse beaucoup je voudrais m’intégrer dans se groupe pour plus de détails
et d’explication sur les cours