
Algèbre de Boole et fonctions Booléennes-Cours et Exercices corrigés
L’algèbre de Boole, ou calcul booléen, est la partie des mathématiques qui s’intéresse aux opérations et aux fonctions sur les variables logiques. Elle fut inventée par le mathématicien britannique George Boole. Aujourd’hui, l’algèbre de Boole trouve de nombreuses applications en informatique et dans la conception des circuits électroniques.
Un circuit électrique, pneumatique, hydraulique peut avoir 2 états logiques. Ces états peuvent prendre la valeur 1 ou 0. C’est ce que l’on appelle la variable logique. Ces états sont fonctions de l’état des composants en série dans le circuit.
- État 0 : Les actionneurs tels que : moteurs, vérins sont à l’état 0 lorsqu’ils ne sont pas alimentés. Le circuit est alors ouvert. Pour un circuit pneumatique ceci correspond à une absence de pression. Pour un circuit électrique cela correspond à une absence de différence de potentiel entre les bornes du circuit. Pour un contact ou un distributeur, c’est l’absence d’action physique intervenant sur un contact qui représente l’état 0.
- État 1 : Les actionneurs sont à l’état 1 lorsqu’ils sont alimentés. Pour un circuit pneumatique ou hydraulique ceci correspond à une pression d’air ou d’huile dans le circuit. Pour un circuit électrique cela correspond à une différence de potentiel entre les bornes du circuit. Pour un contact ou un distributeur ils sont actionnés, c’est à dire qu’une action physique est prise en compte.
Il existe 2 types de logique :
- la logique « positive » : le oui est représenté par un 1, et le non par un 0.
- la logique « négative » : le oui est représenté par un 0, et le non par un 1.
On dispose pour traiter l’information :
- d’un outil mathématique : l’algèbre de Boole, son rôle est de mettre en équation le fonctionnement d’un système, et de le simplifier en vue de sa réalisation physique.
- d’un outil physique : les portes logiques NON -NO-, ET -AND-, OU -OR-, …, fonctions de base « pré-câblées » permettant la fabrication du circuit électrique, pneumatique, ou hydraulique demandé.
Fonctions logiques de base
Il existe 4 fonctions logiques de base
ET: Elle est définie de la manière suivante : a ET b est VRAI si et seulement si a est VRAI et b est VRAI. Cette loi est aussi notée :
- a.b
- a/\b (dans quelques notations algébriques, ou en APL)
- a&b ou a&&b (Perl, C, PHP, …)
- a AND b (Ada, Pascal, Python, …)
| a | b | f | \bar { f } |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
OU : Elle est définie de la manière suivante : a OU b est VRAI si et seulement si a est VRAI ou b est VRAI, ou si a et b sont vrais. Cette loi est aussi notée :
- a+b
- a\/b (dans quelques notations algébriques ou en APL)
- a|b ou a||b (Perl, C, PHP, …)
- a OR b (Ada, Pascal, Python, …)
| a | b | f | \bar { f } |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 |
NON : Le contraire de « a » est VRAI si et seulement si a est FAUX. Le contraire de a est noté :
- \bar { a }
- ~a (dans quelques notations algébriques ou en APL)
- !a (C, C++…)
- NOT a (ASM, Pascal, …)
| a | f |
| 0 | 1 |
| 1 | 0 |
OU EXCLUSIF : f = a ⊕ b
| a | b | f | \bar { f } |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Fonction booléenne (ou logique)
On appelle fonction booléenne une fonction définie sur { 2 }^{ n } combinaisons de n variables logiques.
- Une fonction logique est donc une fonction de n variables logiques,
- Une fonction logique peut prendre en sortie 2 valeurs notées 0 et 1.
Exemple :
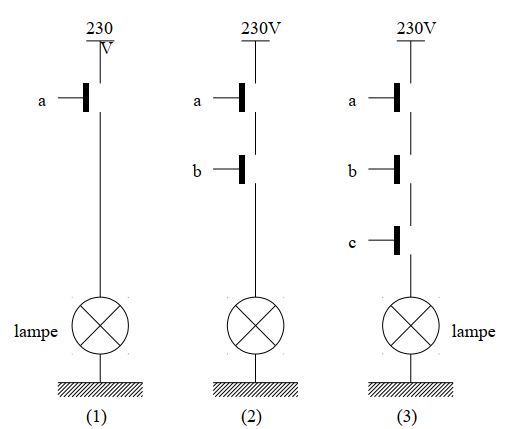
La lampe possède 2 états : allumée -1-, ou éteinte -0-. Cet état est fonction de la position -ouvert 0 ou fermé 1- des différents interrupteurs, a, b et c.
- Les interrupteurs sont les variables logiques. Il y a donc 1 variable dans (1), 2 variables dans (2), ou 3variables dans (3).
- le résultat de la fonction logique est l’état de la lampe, qui possède bien 2 valeurs : allumée -1- ou éteinte -0-.
Une fonction logique peut être représentée par une table donnant pour toutes les combinaisons des états des variables, l’état correspondant de la fonction. Elle comporte { 2 }^{ n } lignes -ou n est le nombre de variable, dans l’ordre binaire naturel. Cette table est appelée table de vérité. Cette table peut être
- totalement définie, c’est-à-dire que l’état de la sortie est parfaitement connue en fonction des variables d’entrées,
- incomplètement définie, c’est-à-dire qu’il existe des états de sortie dits indéterminés, ils traduisent en générale une impossibilité physique. Ils sont notés X dans la table de vérité.
Application
Cas (1) – figure ci-dessus:
- nombre de variable logique : 1
- nombre combinaison pour la fonction de sortie : { 2 }^{ 1 } = 2 états possibles.
- table de vérité :
| a | f |
| 0 | 0 |
| 1 | 1 |
Cas (2) – figure ci-dessus:
- nombre de variable logique : 2
- nombre combinaison pour la fonction de sortie : { 2 }^{ 2 } = 4 états possibles.
- table de vérité :
| a | b | f |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Cas (3) – figure ci-dessus:
- nombre de variable logique : 3
- nombre combinaison pour la fonction de sortie : { 2 }^{ 3 } = 8 états possibles.
- table de vérité :
| a | b | c | f | f’ |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | X |
| 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | X |
| 1 | 1 | 1 | 1 | 1 |
- Fonction incomplètement définie : f’
Règles de l’algèbre de Boole
A- Lois de fermeture :
- a.b = a ET b = variable booléenne définie par la table de vérité de la fonction ET.
- a+b = a OU b = variable booléenne définie par la table de vérité de la fonction OU.
B- Lois de commutativité :
- a.b = b.a
- a+b = b+a
C- Lois d’associativité :
- a.(b.c) = (a.b).c
- a+(b+c) = (a+b)+c
D- Lois d’idempotence :
- a.a = a
- a+a = a
E- Lois de complémentarité :
- a.\bar { a }=0
- a+\bar { fa}=1
F- Lois d’identité remarquable :
- 1.a = a
- 1+a = 1
- 0.a = 0
- 0+a = a
G- Lois de distributivité :
- a.(b+c) = a.b + a.c
- a+(b.c) = (a+b).(a+c)
H- Lois de distributivité « interne » :
- a.b.c = (a.b).(a.c)
- a+(b+c) = (a+b)+(a+c) car a = a+a+a+a+…
G- Exemples :
- x.y+x.\bar { y }=x
- x + x.y = x
- x+\bar { x }.y=x+ y
- x.y+\bar { x }.z+y.z=x.y+\bar { x }.z
- (x+ y).(x+\bar { y })=x
- x.y+x.\bar { y }.z=x.y+x.z
- x.(x+y) = x
- x.(\bar { x }+y)=x.y
H – Théorème de De Morgan (Augustus) :
- \overline { a.b.c }=\bar { a }+\bar { b }+\bar { c }
- \overline { a+b+c }=\bar { a }.\bar { b }.\bar { c }
Représentation des fonctions logiques
A- Écriture algébrique :
On veut utiliser un OU à 4 entrées et 4 ET à 3 entrées. On se propose de simplifier la fonction logique : f =x.y. \bar { z }+x. \bar { y } . z+\bar { x } . y.z+x.y.z
- f =x.y. \bar { z }+x. \bar { y } . z+\bar { x } . y.z+x.y.z
- f =x.y. \bar { z }+x.y.z+x. \bar { y } . z+\bar { x } . y.z
- f =x.y. \bar { z }+x.y.z+x. \bar { y } . z+x.y.z+\bar { x } . y.z+x.y.z
- f =x.y.(z+\bar { z })+x.( \bar { y }+ y). z+(\bar { x }+x). y.z
- f =x.y+x.z+ y.z
B- Écriture par table de vérité :
La fonction vaut 1 si le nombre de 1 est supérieur au nombre de 0.
| a | b | c | f | \bar { f } |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 |
Forme canonique
A- Définition :
C’est l’écriture algébrique de la fonction logique sous la forme de :
- somme de produit, première forme canonique,
- produit de somme, deuxième forme canonique,
- de portes NAND, troisième forme canonique,
- de portes NOR, quatrième forme canonique.
B- Applications :
Si on reprend la fonction du en haut, on peut écrire :
- Première forme canonique, on recherche les combinaisons des variables logiques sous la forme de somme de produit qui amènent la fonction logique à la valeur 1,
f =1 si f =\bar { a }.b.c+a.\bar { b }.c+a.b.\bar { c }+a.b.c
- Deuxième forme canonique, on recherche les combinaisons des variables logiques sous la forme de produit de somme qui amènent la fonction logique à la valeur 0,
f =0 si f = (a+b+c).(\bar { a }+b+c).(a+\bar { b }+c).(a+b+\bar { c })
| a | b | c | 1ère forme appliquée à f=0 | 2ème forme |
| 0 | 0 | 0 | \bar { a }.\bar { b }.\bar { c } | a+b+c |
| 0 | 0 | 1 | \bar { a }.\bar { b }.c | a+b+\bar { c } |
| 0 | 1 | 0 | \bar { a }.b.\bar { c } | a+\bar { b }+c |
| 1 | 0 | 0 | a.\bar { b }.\bar { c } | \bar { a }+b+c |
- Troisième forme canonique, on utilise la première forme canonique mais ici les fonctions logiques sont exprimées à l’aide UNIQUEMENT de portes NAND.
f=\overline { \overline { \bar { a } .b.c+a.\bar { b } .c+a.b.\bar { c } +a.b.c } }
f=\overline { \overline { (\bar { a } .b.c) } .\overline { (a.\bar { b } .c) } .\overline { (a.b.\bar { c } +a.b.c) } }
- Quatrième forme canonique, on utilise la deuxième forme canonique mais ici les fonctions logiques sont exprimées à l’aide UNIQUEMENT de portes NOR
f=\overline { \overline { (a+b+c).(a+b+\bar { c } ).(a+\bar { b } +c).(\bar { a } +b+c) } }
f=\overline { \overline { \overline { (a+b+c) } +\overline { (a+b+\bar { c } ) } +\overline { (a+\bar { b } +c) } +\overline { (\bar { a } +b+c) } } }
Pour plus de détails télécharger les documents ci-dessous:
Liens de téléchargement des cours sur l’Algèbre de Boole et fonctions Booléennes
Cours sur l’Algèbre de Boole et fonctions Booléennes N°1
Cours sur l’Algèbre de Boole et fonctions Booléennes N°2
Cours sur l’Algèbre de Boole et fonctions Booléennes N°3
Cours sur l’Algèbre de Boole et fonctions Booléennes N°4
Cours sur l’Algèbre de Boole et fonctions Booléennes N°5
Cours sur l’Algèbre de Boole et fonctions Booléennes N°6
Cours sur l’Algèbre de Boole et fonctions Booléennes N°7
Cours sur l’Algèbre de Boole et fonctions Booléennes N°8
Cours sur l’Algèbre de Boole et fonctions Booléennes N°9
Liens de téléchargement des exercices corrigés sur l’Algèbre de Boole et fonctions Booléennes
Exercices corrigés sur l’Algèbre de Boole et fonctions Booléennes N°1
Exercices corrigés sur l’Algèbre de Boole et fonctions Booléennes N°2
Exercices sans corrigés sur l’Algèbre de Boole et fonctions Booléennes N°3
Exercices sans corrigés sur l’Algèbre de Boole et fonctions Booléennes N°4
Exercices sans corrigés sur l’Algèbre de Boole et fonctions Booléennes N°5
Exercices sans corrigés sur l’Algèbre de Boole et fonctions Booléennes N°6
Exercices sans corrigés sur l’Algèbre de Boole et fonctions Booléennes N°7