Cercle trigonométrique – Cours et exercices corrigés

Cercle trigonométrique – Cours et exercices corrigés

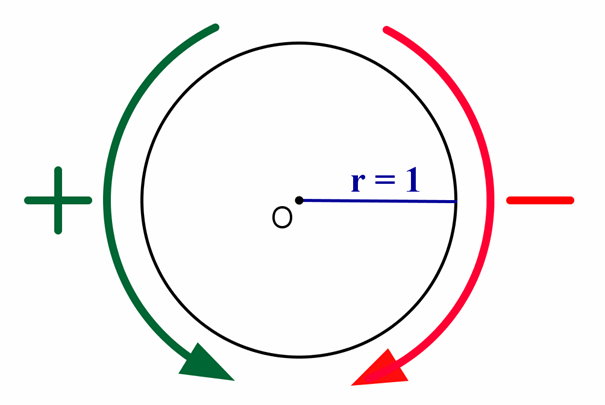
Un cercle trigonométrique est un cercle C de rayon 1 qui est orienté, ce qui veut dire qu’on a choisi un sens positif (celui des ronds-points) et un sens négatif (celui des aiguilles d’une montre) :

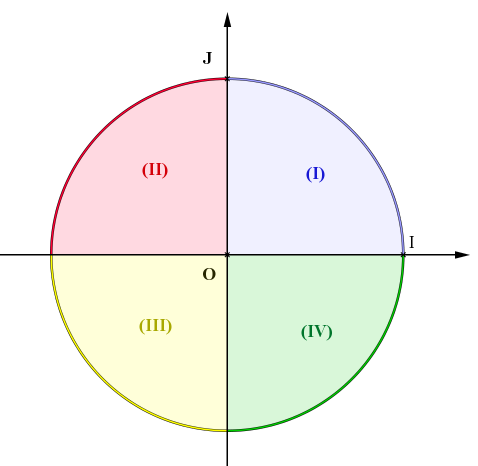
Soit C un cercle trigonométrique de centre O et I, J deux points de C tel que (O,OI,OJ) est un R.O.N. du plan. Alors les axes OI et OJ subdivisent le cercle en quatre quadrants notés : (I), (II), (III) et (IV) :

Soit (T) la tangente à C en I munie du repère (I,OJ ), x ∈ℝ et X(x)∈(T) :

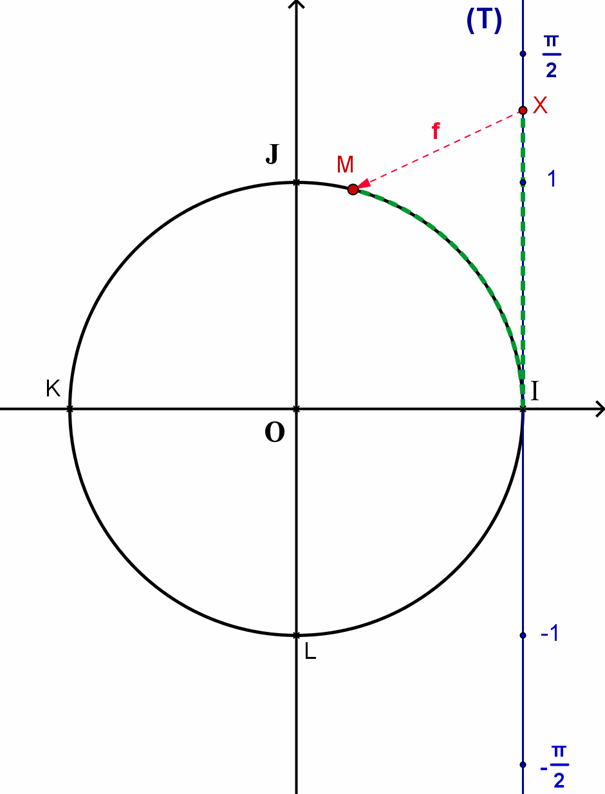
En « enroulant » (T) autour de C à partir du point fixe commun I (vers « le haut » dans le sens positif, vers « le bas » dans le sens négatif), on voit qu’à tout réel x on peut associer un point unique M ∈C . Nous noterons f (x)=M cette correspondance.

De manière générale :

\forall x\in \mathbb{R}, \forall k\in \mathbb{Z}, f(x+k.2\pi)=f(x)

En effet, ajouter k.2π à x revient à faire k tours complets à partir de f (x) = M dans un sens ou dans l’autre (selon le signe de k) pour retomber sur le même point M que x !

Ainsi l’ensemble des nombres x+k .2π (où k ∈ℤ ) caractérise le point M et donc également l’angle IOM . De plus si x ∈[0,2π] alors x est égal à la longueur de l’arc IM  donc tout nombre de la forme x+k .2π est une mesure de la longueur de l’arc IM  à un multiple entier de 2π près ! Ceci nous amène à poser la définition suivante :

Définition

Les nombres x+k .2π (où k ∈ℤ ) sont les mesures en radians (rd) de l’angle IOM et aussi de l’arc IM  . Ainsi :

mes\widehat{IOM}=mes\widehat{IM}= x+2kπ

Exemples :

mes\widehat{IOJ}=\frac{π}{2}+k.2π (k\in \mathbb{Z})

mes\widehat{IOK}=\pi +k.2\pi (k\in \mathbb{Z})

mes\widehat{IOL}=\frac{3\pi}{2}+k.2\pi  (k\in \mathbb{Z})

Chaque angle a donc:

• une infinité de mesures, mais la différence entre deux mesures est toujours un multiple entier de 2π si on mesure en rd, un multiple entier de 360 si on mesure en degrés.,
• une seule mesure comprise entre 0 rd et 2π rd : c’est la plus petite mesure positive.
• une seule mesure comprise entre −π rd et π rd : c’est la mesure principale.

Correspondance entre degrés et radians :

Les transformations se font par une règle de trois :

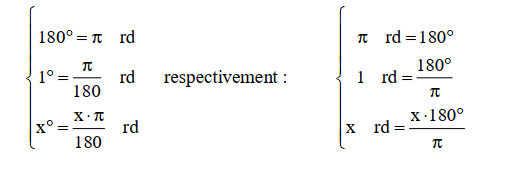
Exemples :

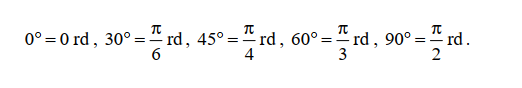
Pour plus de détails télécharger les documents ci-dessous:

Liens de téléchargement des cours sur le Cercle trigonométrique

Liens de téléchargement des exercices corrigés sur le Cercle trigonométrique

Voir aussi :

Autres sujets peuvent vous intéresser

Partagez au maximum pour que tout le monde puisse en profiter