
Loi d’Ohm – Cours et exercices corrigés
La loi d’ohm établit une relation entre la valeur d’une résistance, la tension qu’elle reçoit et l’intensité du courant qui circule.
I- Énoncé de la loi d’ohm
| Lorsqu’un courant d’intensité I traverse un conducteur ohmique de résistance R, la tension à ses bornes est : U = R.I |
Avec :
- U est exprimé en V
- R est exprimé en Ω
- I est exprimé en A
Cette relation est appelée loi d’Ohm.
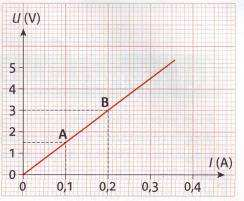
La représentation graphique U= f(I) de cette caractéristique est une droite passant par l’origine, ce qui signifie que U et I sont proportionnels.
II- Utilisation de la loi d’Ohm
II-1- Par le calcul
Cette loi étant valable pour tout dipôle ohmique, on peut s’en servir pour calculer
- U, si on connaît la valeur de I et de R : formule U = R×I
- R, si on connaît la valeur de U et de I : formule R =U/I
- I, si on connaît la valeur de U et de R : formule I =U/R
II-2- Par le graphique
On peut également utiliser la représentation graphique de la caractéristique du dipôle ohmique :
- On peut par exemple calculer la résistance de ce dipôle ohmique car au point A on a U = 1.5 V et I = 0.1 A donc R = U/I = 1.5/0.1= 15 Ω.
Sinon on peut nous donner la valeur de la résistance correspondant à la caractéristique tracée (figure ci-dessous) et nous demandait à quelle intensité correspond une tension de 3V par exemple : cela donne I = 0.2 A (pour cette résistance). Il suffit de savoir lire un graphique.
III- Caractéristique d’un dipôle non ohmique
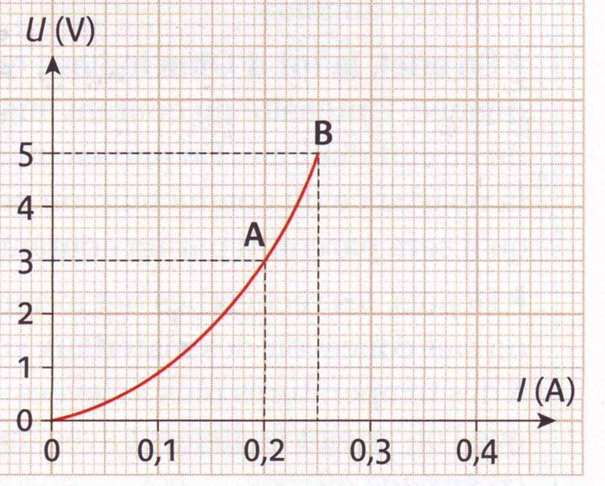
Un dipôle n’est pas ohmique, lorsqu’il ne vérifie pas la loi d’ohm U = R×I.
La résistance R de ce dipôle n’est plus constante, la caractéristique de ce dipôle n’est plus une droite.
Remarque : En générale, la résistance d’un dipôle dépend de la température, et comme par exemple une lampe chauffe beaucoup pour assurer sa fonction d’éclairage …
IV- Exercices
1- Exercice 1 sur la Loi d’Ohm
On trace les caractéristiques de deux dipôles. Lequel a la résistance la plus élevée ? Justifier par le calcul.
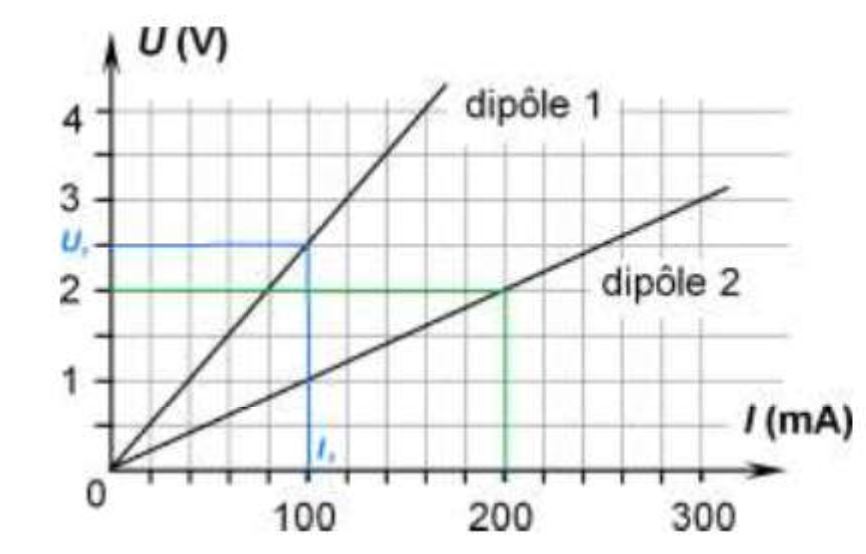
Correction
La courbe caractéristique du dipole 1 passe par le point (U1 ;I1) soit (2.5V ; 100 mA).
- Conversion 100mA = 0.1A
- Donc R1=U1/I1 = 2.5/0.1 = 25Ω
- De même , R2=U2/I2 = 2/0.2 = 10 Ω
D’où R1>R2
2- Exercice 2 sur la Loi d’Ohm
L’intensité du courant traversant un conducteur ohmique de 27Ω est de 222 mA. Calculer la tension appliquée entre ses bornes.
Correction
Soit R= 27Ω et I= 222 mA (Conversion : I=0.222 A)
On a la loi d’Ohm U= R.I = 27 × 0.222
D’où U=6V
3- Exercice 3 sur la Loi d’Ohm
Un dipole ohmique de résistance 3300Ω est détérioré si l’intensité du courant qui le traverse est supérieure à 25 mA.
Quelle tension maximale peut-on appliquer entre les bornes du dipôle sans le détériorer ?
Correction
Ici, R = 3300Ω et Imax = 25 mA ( Conversion : Imax = 0.025 A)
Umax = R × Imax = 3300 × 0.025
D’où Umax = 82.5 V
4- Exercice 4 sur la Loi d’Ohm
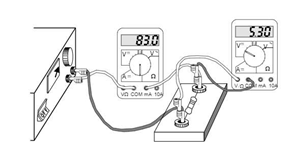
a- Dans quel but a-t-on réalisé le montage ci-dessus ?
b- Faire le schéma normalisé de ce circuit ?
c- que vaut, en ohms, la résistance du dipole ohmique étudié? attention, l’écran de l’ampèremètre affiche ici des mA!
Correction
a- ce montage est celui qui est réalisé lorsqu’on veut mesurer le courant qui traverse un dipôle ohmique et la tension à ses bornes.
Ces valeurs, variables, permettent de tracer la courbe caractéristique de ce dipôle.
b-
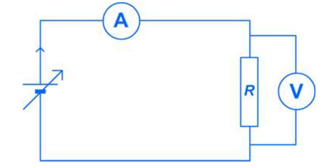
c- le voltmètre affiche U=5.3 V
L’ampèremètre affiche I = 83 mA ( conversion : 0.083 A)
Selon à la loi d’ohm U = R x I donc R = U / I = 5.3/0.083
D’où R= 63.9 Ω
This is such a great watch! It’s stunning and so heavy! Highly recommended!
C’est tres necessaire voir sur cet platforme de livre interestessant