Théorème de THALES – Cours et Exercices corrigés

Théorème de THALES – Cours et Exercices corrigés

Théorème de THALES – Cours et Exercices corrigés

I- Théorème de THALES
I-1 Enoncé du Théorème de Thalès :
  • Soit ABC un triangle non aplati
  • Soit M un point de la demi-droite [AB), distinct de A.
  • Soit N un point de la demi-droite [AC), distinct de A.
  • Si la droite (MN) est parallèle à la droite (BC) alors
AMAB=ANAC=MNBC \frac { AM }{ AB } =\frac { AN }{ AC } =\frac { MN }{ BC }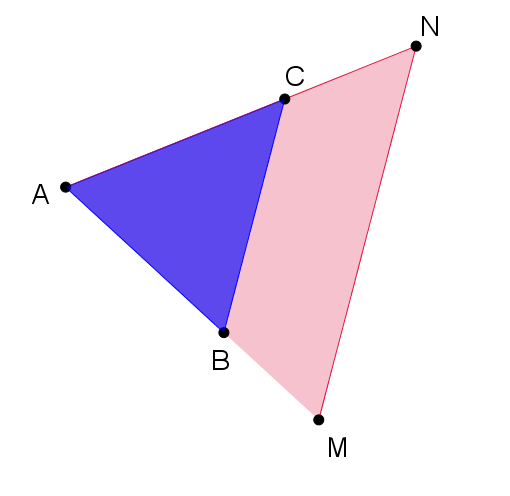
Théorème de THALES
Théorème de THALES
I-2 Exemples :
a- Exemple 1
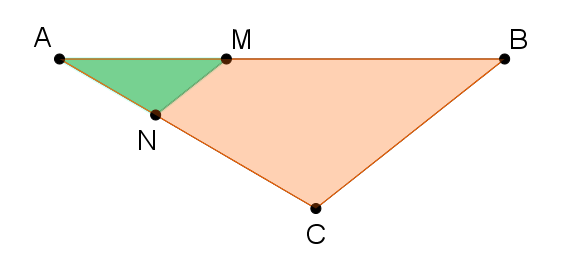
Théorème de THALES

AM = 30; AB = 80; AC = 20. Les droites (MN) et (BC) sont parallèles. Calculer AN.

Réponse :

Les droites (MN) et (BC) étant parallèles, on peut appliquer le théorème de Thalès dans les triangles AMN et ABC :

AMAB=ANAC=MNBC \frac { AM }{ AB } =\frac { AN }{ AC } =\frac { MN }{ BC }
Soit3080=AN20=MNBC Soit \quad \frac { 30 }{ 80 } =\frac { AN }{ 20 } =\frac { MN }{ BC }
DoncAN×80=30×20Donc \quad AN \times 80 = 30 \times 20
SoitAN=30×2080=304=7.5 Soit \quad AN = \frac { 30 \times 20 }{ 80 } =\frac { 30 }{ 4 } = 7.5
b- Exemple 2
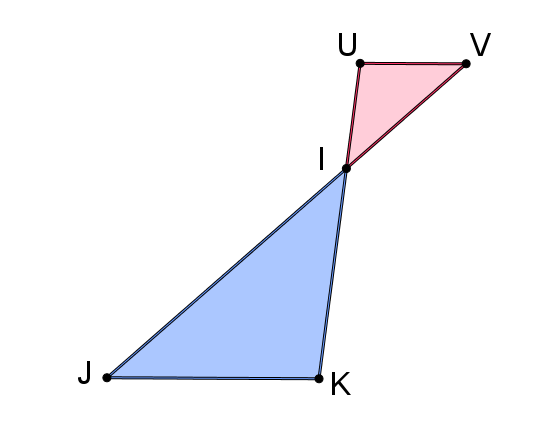
Théorème de THALES

(UV) // (JK). IJ = 30 ; IK = 20 ; IU = 10 ; UV = 10. Calculer IV et JK.

Réponse :

Les droites (UV) et (JK) étant parallèles, on peut appliquer le théorème de Thalès dans les triangles IUV et IJK :

IJIV=IKIU=JKUV \frac { IJ }{ IV } =\frac { IK }{ IU } =\frac { JK }{ UV }
Soit30IV=2010=JK10Soit \quad \frac { 30 }{ IV } =\frac { 20 }{ 10 } =\frac { JK }{ 10 }
DoncIV=1020×30=15etJK=2010×10=20Donc \quad IV= \frac { 10 }{ 20 } \times30=15 \quad et \quad JK= \frac { 20 }{ 10 } \times10=20
II- Réciproque du Théorème de Thalès
II-1 Enoncé de la réciproque du Théorème de THALES

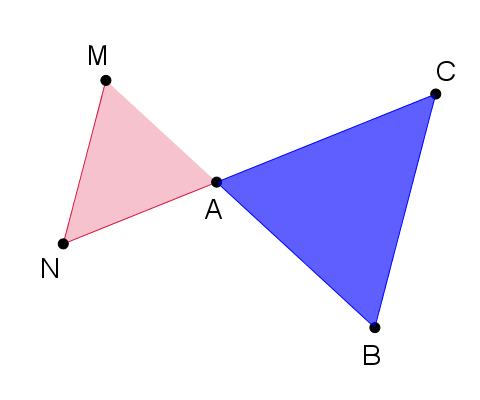
Si ABC et AMN sont deux triangles tels que

A, M, B et A, N, C sont alignés dans cet ordre

etAMAB=ANACet \quad \frac { AM }{ AB } =\frac { AN }{ AC }

Alors, les droites (MN) et (BC) sont parallèles

II-1 Exemples
a- Exemple 1
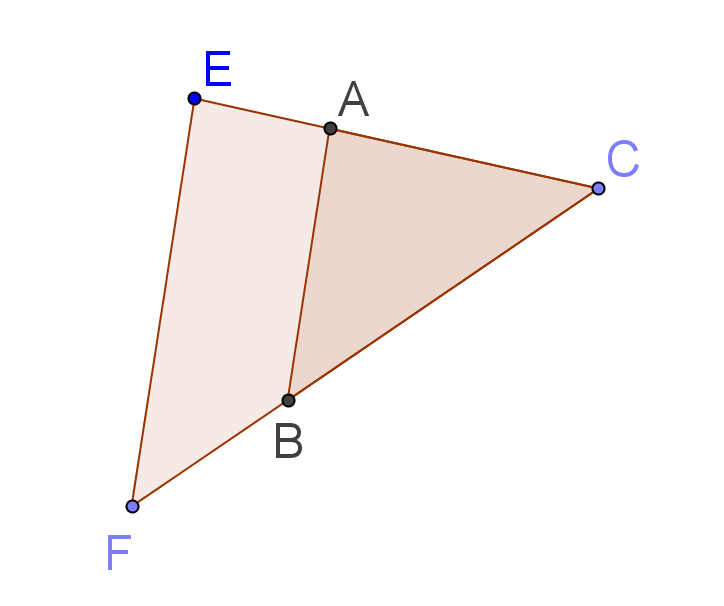
Réciproque de Thalès
  • AC = 11 ; AE = 22 ;
  • CB = 15 ; CF = 30.
  • Les droites (AB) et (EF) sont-elles parallèles ?
Réponse :
D′unepartCACE=1133=13D'une part \quad \frac { CA }{ CE } =\frac { 11 }{ 33 } =\frac { 1 }{ 3 }
etd′autrepartCBCF=1545=13et \quad d'autre\quad part \quad\quad \frac { CB }{ CF } =\frac { 15 }{ 45 } =\frac { 1 }{ 3 }
DoncCACE=CBCFDonc \quad \frac { CA }{ CE } = \frac { CB }{ CF }

CAB et CEF sont deux triangles tels que C, A, E et C, B, F sont alignés dans cet ordre et CA/CE=CB/CF, donc selon la réciproque du théorème de Thalès les droites (AB) et (EF) sont parallèles.

b- Exemple 2 :
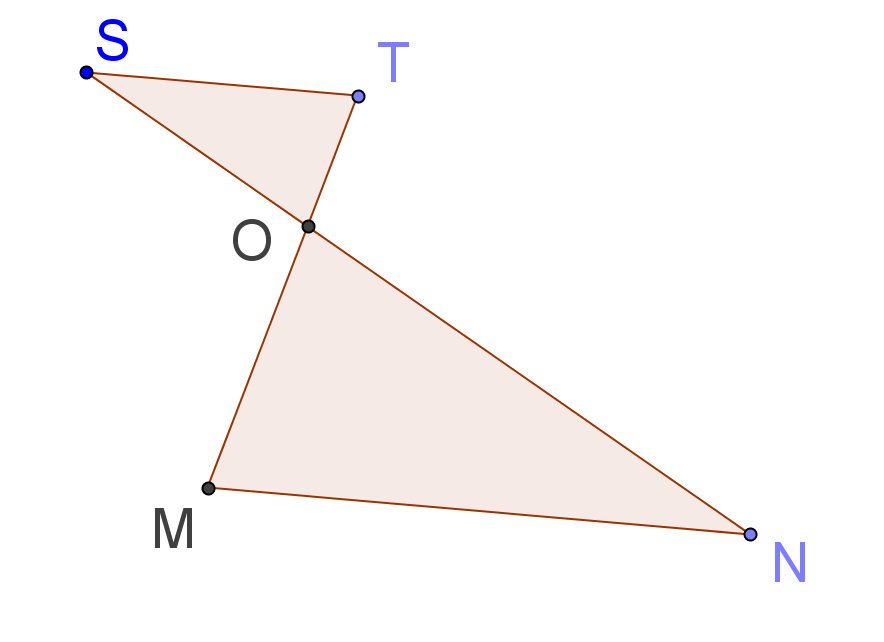
Réciproque du Théorème de_Thalès

Démontre que les droites (MN) et (ST) sont parallèles.
On donne OM = 2,8 cm ; ON = 5,4 cm ; OS = 2,7 cm et OT = 1,4 cm.

Réponse :
OTOM=1.42.8=12etOSON=2.75.4=12\frac { OT }{ OM } =\frac { 1.4 }{ 2.8 } =\frac { 1 }{ 2 } \quad et \quad \frac { OS }{ ON } =\frac { 2.7 }{ 5.4 } =\frac { 1 }{ 2 }

OST et ONM sont deux triangles tels que S, O, N et T, O, M sont alignés dans cet ordre et OT/OM = OS/ON, donc selon la réciproque du théorème de Thalès les droites (MN) et (ST) sont parallèles.

III- Conséquence du théorème de Thalès : montrer que deux droites ne sont pas parallèles

Si ABC et AMN sont deux triangles tels que :

A, M, B et A, N, C sont alignés dans cet ordre

etAMAB≠ANACet \quad \frac { AM }{ AB } \neq \frac { AN }{ AC }

alors, les droites (MN) et (BC) ne sont pas parallèles

Exemple :
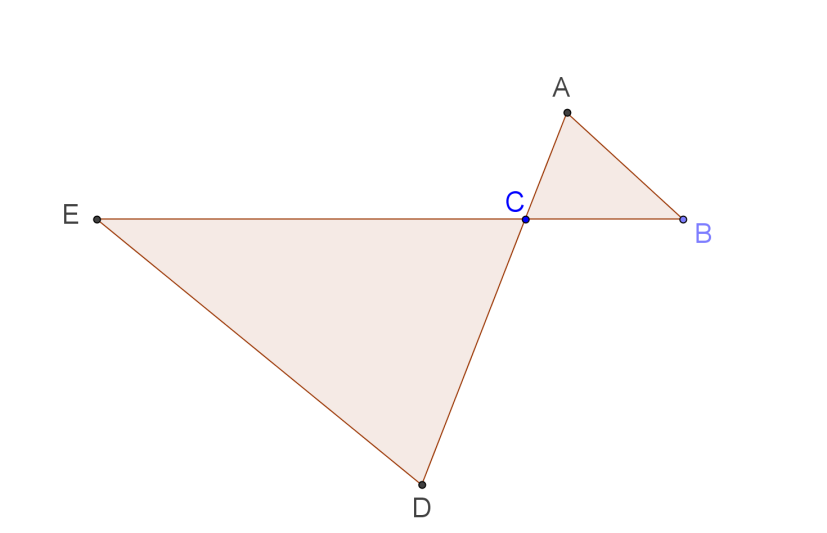
Montrer que deux droites ne sont pas parallèles

On donne AB = 2,5 cm ; BC = 3,3 cm ; AC = 2,4 ; CD = 6 cm et CE = 9 cm. Les droites (ED) et (AB) sont-elles parallèles? Justifie la réponse.

Réponse :
CACD=2.46=25etCBCE=3.39=1130\frac { CA }{ CD } =\frac { 2.4 }{ 6 } =\frac { 2 }{ 5 } \quad et \quad \frac { CB }{ CE } =\frac { 3.3 }{ 9 } =\frac { 11 }{ 30 }
Or25=1230≠1130doncCACD≠CBCEOr\quad \frac { 2 }{ 5 } =\frac { 12 }{ 30 } \neq\frac { 11 }{ 30 } \quad donc \quad \frac { CA }{ CD } \neq\frac { CB }{ CE }

CAB et CDE sont deux triangles tels que A, C, D et B, C, E sont alignés dans cet ordre et CA/CD # CB/CE, donc selon la conséquence du théorème de Thalès les droites (ED) et (AB) ne sont pas parallèles.

Remarque : la conséquence du théorème de Thalès se nomme aussi la contraposée du théorème de Thalès.

Pour plus de détails télécharger les documents ci-dessous:

Liens de téléchargement des cours sur le Théorème de THALES

Cours sur le Théorème de THALES N°1

Télécharger

Cours sur le Théorème de THALES N°2

Télécharger

Cours sur le Théorème de THALES N°3

Télécharger

Cours sur le Théorème de THALES N°4

Télécharger

Cours sur le Théorème de THALES N°5

Télécharger

Cours sur le Théorème de THALES N°6

Télécharger

Cours sur le Théorème de THALES N°7

Télécharger

Liens de téléchargement des exercices corrigés sur le Théorème de THALES

Exercices corrigés sur le Théorème de THALES N°1

Télécharger

Exercices corrigés sur le Théorème de_THALES N°2

Télécharger

Exercices corrigés sur le Théorème de_THALES N°3

Télécharger

Voir aussi :

Théorème de Pythagore-Cours et Exercices corrigés

Dénombrement : Cours-Résumés-Exercices corrigés

Probabilité : Cours-Résumés -Exercices-corrigés

Produit scalaire : Cours-Résumés-Exercices corrigés

Dérivées : Cours-Résumés-Exercices corrigés

Produit vectoriel : Cours – Résumés – Exercices

Partagez au maximum pour que tout le monde puisse en profiter
Étiquettes
Merci de partager cet article avec vos amis

Publications similaires

Un commentaire

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *