
La gravitation universelle : Cours et Exercices corrigés
La gravitation universelle est une des interactions responsable de la cohésion de l’univers. Elle est prédominante à l’échelle astronomique. C’est elle qui explique la cohésion et la structure du système solaire. Elle est la cause du mouvement des planètes et de leurs satellites.
I- Interactions gravitationnelles
I.1 Définition
Deux corps A et B sont en interaction gravitationnelle s’ils exercent mutuellement, l’un sur l’autre, des forces d’attraction dues au seul fait qu’ils ont une masse non nulle.
I.2. Expression de la force de gravitation (loi de Newton)
Deux corps ponctuels A et B, de masses mA et mB, séparés par une distance d, exercent l’un sur l’autre des forces d’interactions gravitationnelles attractives :
{ F }_{ A/B } \quad et \quad { F }_{ B/A }Ayant :
- même droite d’action (AB)
- des sens opposés
- même intensité (ou valeur) :
{ F }_{ A/B }={ F }_{ B/A }=G\frac { { m }_{ A }.{ m }_{ B } }{ { d }^{ 2 } } G : constante de gravitation universelle
Unités SI :
- mA et mB en kilogrammes (kg)
- d en mètres (m)
- G = 6.67. 10 -11 m 3. kg -1. s -2
Remarque : cette loi est aussi valable pour des corps volumineux présentant une répartition sphérique de masse (même répartition de masse autour du centre de l’objet). C’est le cas des planètes et des étoiles, la distance d est celle qui sépare leurs centres.
1.3. Représentation par un vecteur
Une force peut être représentée par un vecteur ayant pour direction, la droite d’action de la force, pour sens, celui de la force, pour origine, le point d’application de la force et une longueur (ou norme) proportionnelle à l’intensité de la force.
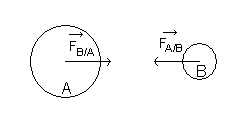
Il faut choisir une échelle de représentation adaptée.
II- Poids d’un corps et force gravitationnelle
II.1. Poids d’un corps
Le poids d’un corps est la force d’attraction qu’il subit lorsqu’il est situé à la surface de la Terre ou, à proximité de sa surface. Le poids d’un corps est essentiellement à la force de gravitation que la Terre exerce sur lui.
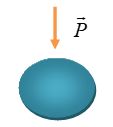
II.2. Caractéristiques du poids
Les caractéristiques du poids sont :
- direction : la verticale
- sens : de haut en bas (vers le centre de la Terre)
- intensité (ou valeur) : P = m. g
II.3. Expression de l’ intensité de la pesanteur
Le poids P d’un objet peut-être identifié à la force de gravitation F exercée par la Terre sur cet objet :
P=F=m.g \quad{ F }=m.G\frac { { M }_{ T } }{ { { ({ R }_{ T }+h) }^{ 2 } } } \quad on \quad pose \quad d = { R }_{ T }+hAlors \quad m.g=m.G\frac { { M }_{ T } }{ { { ({ R }_{ T }+h) }^{ 2 } } } L'expression \quad de \quad l’ intensité \quad de \quad la \quad pesanteur \quad est \quad g=G\frac { { M }_{ T } }{ { { ({ R }_{ T }+h) }^{ 2 } } } Remarque : – cette expression est aussi valable a la surface de la terre (h=0) on obtient :
{ g }_{ 0 }=G\frac { { M }_{ T } }{ { { { R }_{ T } }^{ 2 } } } - m : masse de l’objet en kg
- g : intensité de la pesanteur en N.kg-1
III- L’ordre de grandeur
III .1 Définition de l’ordre de grandeur.
La notation scientifique est l’écriture d’un nombre sous la forme du produit : a.10n
Avec a : nombre décimal 1 <= a < 10 et n, entier positif ou négatif
Si a < 5 alors l’ordre de grandeur du nombre est 10n : .
Si a >=5 alors l’ordre de grandeur est 10n+1
Exemple
| distance en mètre (notation scientifique) | ordre de grandeur | |
|---|---|---|
| Terre-Lune | 380 000 km =3,8.108 m | 108 m |
| Rayon atome d’hydrogène | 0,105 nm=1,05.10-10 m | 10-10 m |
| Dimension d’une molécule | 2 nm=2.10-9 m | 10-9 m |
| Rayon de la Terre | 6400 km=6,4.106 m | 107 m |
| Taille d’un homme | 170 cm=1,70 m | 100 = 1 m |
III.2 Comparaison de deux valeurs numériques
Pour comparer les valeurs prises par une grandeur physique (Exemples : une masse une longueur) , il faut les convertir dans la même unité.
Deux valeurs seront du même ordre de grandeur si le quotient de l’ordre de grandeur de la plus grande par la plus petite est compris entre 1 et 10.
Pour plus de détails télécharger les documents ci-dessous:
Liens de téléchargement des cours sur la gravitation universelle
Cours sur la gravitation universelle N°1
Cours sur la gravitation universelle N°2
Cours sur la gravitation universelle N°3
Cours sur la gravitation universelle N°4
Cours sur la gravitation universelle N°5
Cours sur la gravitation universelle N°6
Cours sur la gravitation universelle N°7
Liens de téléchargement des exercices corrigés sur la gravitation universelle
Exercices corrigés sur la gravitation universelle N°1
Exercices corrigés sur la gravitation universelle N°2
There is evidently a bunch to realize about this. I think you made various good points in features also. Romonda Julian Fawcette
Really appreciate you sharing this blog post. Really looking forward to read more. Fantastic. Timmy Zaccaria Anabelle
Yes! Finally something about eddm prining near me. Cloe Zebulen Bolt