
Mécanique du point matériel : Cours, résumé, exercices et examens corrigés.
- Introduction
- Système de coordonnées
- Plan du cours N°1 de mécanique du point matériel
- Plan du cours N°2 de mécanique du point_matériel
- Liens de téléchargement des cours et résumé sur la mécanique du point matériel
- Liens de téléchargement des exercices et examens corrigés sur la mécanique du point matériel
- Voir aussi :
Introduction
La mécanique du point concerne les objets matériels dont l’extension spatiale est très faible : leurs déformations et l’énergie liée à leur mouvement propre de rotation peuvent ainsi être négligées devant les énergies mises en jeu. Cependant un objet aussi volumineux que la terre ou le soleil peut dans certains cas être assimilable à un point en ce qui concerne, par exemple, son action sur des corps dans son entourage.
Système de coordonnées
Pour quantifier les mesures, le plus évident consiste à prendre un système d’axes orthonormé lié au repère qui permettra de déterminer les composantes du mouvement (position, vitesse …) et des forces. Mais ce n’est pas la seule possibilité. De nombreux problèmes sont plus simples en utilisant un système de coordonnées cylindrique, sphérique …
Dans tous les cas il faudra définir une origine et 3 vecteurs unitaires qui définiront les directions des axes. Ces vecteurs constituent la base.
1- Système de coordonnées cartésiennes
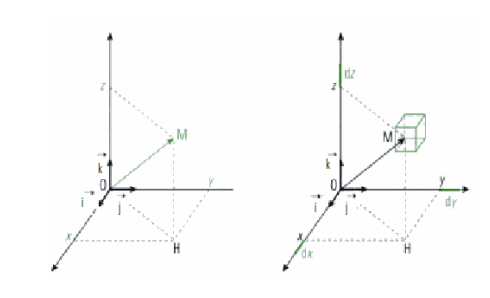
Chaque position est repérée par ses coordonnées. S’il s’agit d’un repère linéaire par une seule coordonnée (x), d’un repère plan par deux coordonnées (x,y) et dans l’espace par trois coordonnées (x,y,z). ces coordonnées sont les projection de la position sur chaque axe doté d’un vecteur unitaire.
La position peut être exprimée par un vecteur position qui lie l’origine du repère choisi à la position.
Le repère est orthonormé, c’est-à-dire que les vecteurs unitaires sont normés à l’unité et orthogonaux entre eux.
2- Système de coordonnées cylindrique
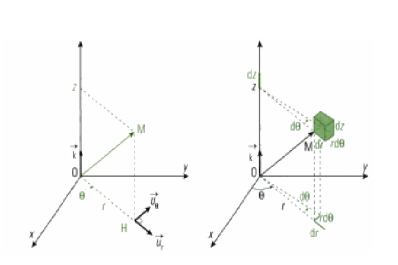
Si le mouvement du point M est circulaire dans le plan (XOY) et translate suivant l’axe (OZ) on repère la position M par les coordonnées cylindriques (r,θ, z).
– r : représente la distance du point M à l’axe Oz ;
– θ : Définit la position du point M autour de Oz (θ angle compris entre 0 et 2π) ;
– z : représente la cote du point M.
3- Système de coordonnées sphériques
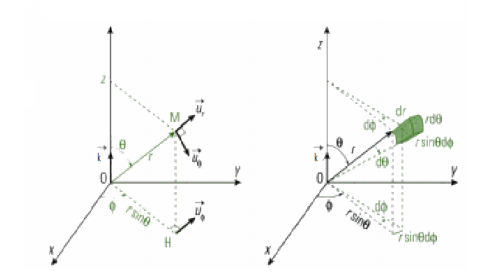
Si le mouvement de M est circulaire suivant tous les axes on utilise les coordonnées sphériques (r, θ, φ)
– r : représente la distance du point M à l’origine O ;
– θ et φ : définissent la direction dans laquelle, depuis le point O, on voit le point M (θ angle compris entre O et π, φ angle compris entre 0 et 2π).
Plan du cours N°1 de mécanique du point matériel
I – Système de coordonnées – Cinématique du point matériel (avec et sans changement de référentiel).
II – Loi fondamentale et théorèmes généraux de la dynamique du point matériel.
III – Travail et énergie.
IV – Les mouvements à force centrale.
V – Vibrations simples : Systèmes à un degré de liberté.
VI -Chocs de deux particules.
Plan du cours N°2 de mécanique du point_matériel
Calcul vectoriel
Analyse dimensionnelle
Calcul d’incertitude
Cinématique
Mouvement relatif
Dynamique
Travail et énergie
Liens de téléchargement des cours et résumé sur la mécanique du point matériel
Cours N°1 de mécanique du point matériel
Cours N°2 de mécanique du point matériel
Cours N°3 de mécanique_du_point matériel
Cours N°4 de mécanique_du_point matériel
Cours et exercices N°5
Cours et exercices N°6
Résumé de mécanique du point matériel
Liens de téléchargement des exercices et examens corrigés sur la mécanique du point matériel
Exercices N°1
Exercices et contrôles corrigés N°2
Exercices N°3
Exercices N°4
Exercices N°5
Exercices N°6
Exercices N°7
Examens N°1
Examens N°2
Voir aussi :
Autres sujets peuvent vous intéresser
Partagez au maximum pour que tout le monde puisse en profiter