Fonction exponentielle – Cours, résumés et exercices corrigés

Fonction exponentielle : Cours, résumé et exercices corrigés

I- Théorème 1

Soit f une fonction dérivable sur R telle que

f′ = f et f(0) = 1.

Alors, pour tout réel x, f(x) × f(−x) = 1. En particulier, la fonction f ne s’annule pas sur R

Démonstration.

Soit f une fonction dérivable sur R telle que f′ = f et f(0) = 1.

Soit g la fonction définie sur R par : pour tout réel x, g(x) = f(x) × f(−x).

La fonction g est dérivable sur R en tant que produit de fonctions dérivables sur R et pour tout réel x,

g′(x) = f′(x) × f(−x) + f(x) × (−1) × f′(−x) = f′(x)f(−x) − f(x)f′(−x)

= f(x)f(−x) − f(x)f(−x) (car f′ = f)

= 0.

Ainsi, la dérivée de la fonction g est nulle. On sait alors que la fonction g est une fonction constante sur R.

Par suite, pour tout réel x, g(x) = g(0) = (f(0))² = 1.

On a montré que pour tout réel x, f(x)×f(−x) = 1. En particulier, pour tout réel x, f(x)×f(−x) ≠ 0 puis f(x) ≠ 0.

Ainsi, une fonction f telle que f′ = f et f(0) = 1 ne s’annule pas sur R.

II- Théorème 2

Soient f et g deux fonctions dérivables sur R telles que f′ = f, g′ = g, f(0) = 1 et g(0) = 1.

Alors, f = g

Démonstration

Soient f et g deux fonctions dérivables sur R telles que f′ = f, g′ = g, f(0) = 1 et g(0) = 1.

D’après le théorème 1, la fonction g ne s’annule pas sur R. On peut donc poser h = f / g.

La fonction h est dérivable sur R en tant que quotient de fonctions dérivables sur R dont le dénominateur ne s’annule pas sur R et pour tout réel x,

h^{'}(x)=\frac{f^{'}(x)g(x)-f(x)g^{'}(x)}{(g(x))^{2}}=\frac{f(x)g(x)-f(x)g(x)}{(g(x))^{2}}=0

La dérivée de h est nulle sur R. La fonction h est donc constante sur R.

Par suite, pour tout réel x,

h(x)=h(0)=\frac{f(0)}{g(0)}=\frac{1}{1}=1

Ainsi, pour tout réel x, f(x)/g(x) = 1 ou encore, pour tout réel x, f(x) = g(x). On a montré que f = g ou encore on a montré l’unicité d’une fonction f vérifiant la relation f′ = f et f(0) = 1

III- Définition

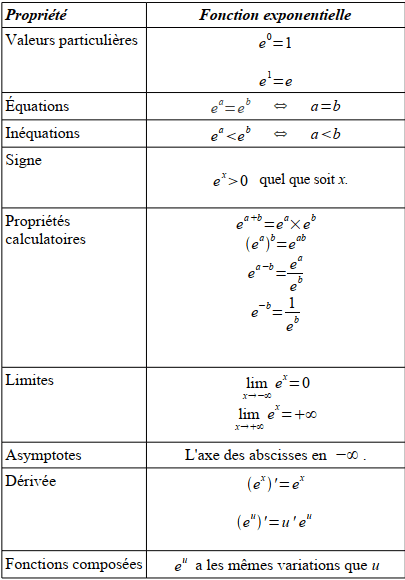
La fonction exponentielle est l’unique fonction définie et dérivable sur R, égale à sa dérivée et prenant la valeur 1 en 0.

Pour tout réel x, l’exponentielle du réel x est notée exp(x). Par définition, pour tout réel x, exp′(x) = exp(x) et exp(0) = 1.

IV- Propriétés algébriques de la fonction exponentielle

1- Relation fonctionnelle

Pour tous réels x et y, exp(x+y) = exp(x) × exp(y).

Donc si f est la fonction exponentielle de base exp alors f(x+y) = f(x) f(y), on dit que les fonctions exponentielles transforment une somme en un produit.

2- Le nombre e. Changement de notation

e = exp(1) = 2, 718 . . ..

3- Propriétés algébriques de la fonction exponentielle

Pour tous réels x et y,

a- Propriétés algébriques N°1

exp(-x)=\frac{1}{exp(x)}

Démonstration :

exp(x)\times exp(-x)=exp(x-x)=1 \: donc exp(-x)=\frac{1}{exp(x)}

b- Propriétés algébriques N°2

exp(x-y)=\frac{exp(x)}{exp(y)}

Démonstration :

exp(x-y)=exp(x+(-y))=exp(x)\times exp(-y)=\frac{exp(x)}{exp(y)}

c- Propriétés algébriques N°3

exp(x)^{y}=exp(xy)

Démonstration :

Si b est un nombre positif

exp(x)^{y}=exp(x)\times exp(x)\times exp(x)\times exp(x)\times....\times exp(x) = exp(x+x+x+....+x)= exp(xy)

Si b est un nombre négatif, alors -b est un nombre positif

exp(xy)=exp(x(-(-y))) \: or \:exp(x(-y))=exp(-xy)

D’après ce qui précède donc

exp(xy)=exp(-(-xy))=exp(xy)

d- Propriétés algébriques N°4

Pour tout entier naturel n, exp(1/n) est le nombre qui à la puissance n est égal à e.

Donc tel que:

exp(\frac{1}{n})^{n}=e

Démonstration :

exp(\frac{1}{n})^{n}=exp(\frac{1}{n}\times n)=exp(1)=e

V- Propriétés analytiques de la fonction exponentielle

1- Sens de variation de la fonction exponentielle

La fonction exponentielle est strictement positive sur R.
La fonction exponentielle est strictement positive sur R.
Pour tous réels x et y, exp(x) < exp(y) ⇔ x < y.
Pour tous réels x et y, exp(x) = exp(y) ⇔ x = y.
Pour tout réel x, exp(x) > 1 ⇔ x > 0, exp(x) = 1 ⇔ x = 0, exp(x) < 1 ⇔ x < 0.

Exercice:

Résoudre dans R l’équation exp(−5x+1) = 1.
Résoudre dans R l’équation exp(2x) = 0.
Résoudre dans R l’équation exp(x2) = exp(4).

Solution

1) Soit x un réel

exp(-5x+1)=1\Leftrightarrow -5x+1=0\Leftrightarrow x=\frac{1}{5}

L’ensemble des solutions de l’équation exp(−5x+1) = 1 est : 1/5

2) La fonction exponentielle est strictement positive sur R. Donc l’équation exp(2x) = 0 n’a pas de solution

3) Soit x un réel

exp(x^{2})=exp(4)\Leftrightarrow x^{2}=4\Leftrightarrow x=-2 \:ou \: x=-2

L’ensemble des solutions de l’équation exp(x2) = exp(4 est : {-2;2}

2- Limites de la fonction exponentielle en −∞ et +∞

\lim_{x\rightarrow +\infty }exp(x)=+\infty

\lim_{x\rightarrow -\infty }exp(x)=0

\lim_{x\rightarrow +\infty }\frac{exp(x))}{x}=+\infty

\lim_{x\rightarrow -\infty }x.exp(x)=0

Exercice

Calculer les limites suivantes:

1- \: \lim_{x\rightarrow +\infty }(exp(x)+x+1))

2- \: \lim_{x\rightarrow -\infty }(exp(x)+x+1))

1- \:\lim_{x\rightarrow -\infty }x^{2}exp(-2x+3)

Solution

1- On a :

\lim_{x\rightarrow +\infty }exp(x)=+\infty

Et d’autre part :

\lim_{x\rightarrow +\infty }x+1=+\infty

En additionnant les deux fonctions, on obtient:

\lim_{x\rightarrow +\infty }(exp(x)+x+1))=+\infty

2- On a :

\lim_{x\rightarrow -\infty }exp(x)=0

Et d’autre part :

\lim_{x\rightarrow -\infty }x+1=-\infty

En additionnant les deux fonctions, on obtient:

\lim_{x\rightarrow -\infty }(exp(x)+x+1))=-\infty

3- On a

\lim_{x\rightarrow -\infty } (-2x+3)=+\infty

\lim_{x\rightarrow -\infty } exp(-2x+3)=\lim_{x\rightarrow +\infty } exp(X)=+\infty

Et d’autre part :

\lim_{x\rightarrow -\infty }x^2=+\infty

En multipliant les deux fonctions, on obtient

\lim_{x\rightarrow -\infty }x^{2}exp(-2x+3)=+\infty

3- Graphe de la fonction exponentielle

On connaît déjà le sens de variation de la fonction exponentielle ainsi que les limites de cette fonction en −∞ et +∞. On peut résumer ces différents résultats dans un tableau de variations suivant:

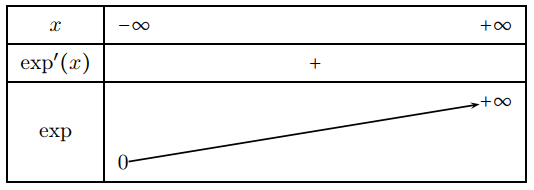
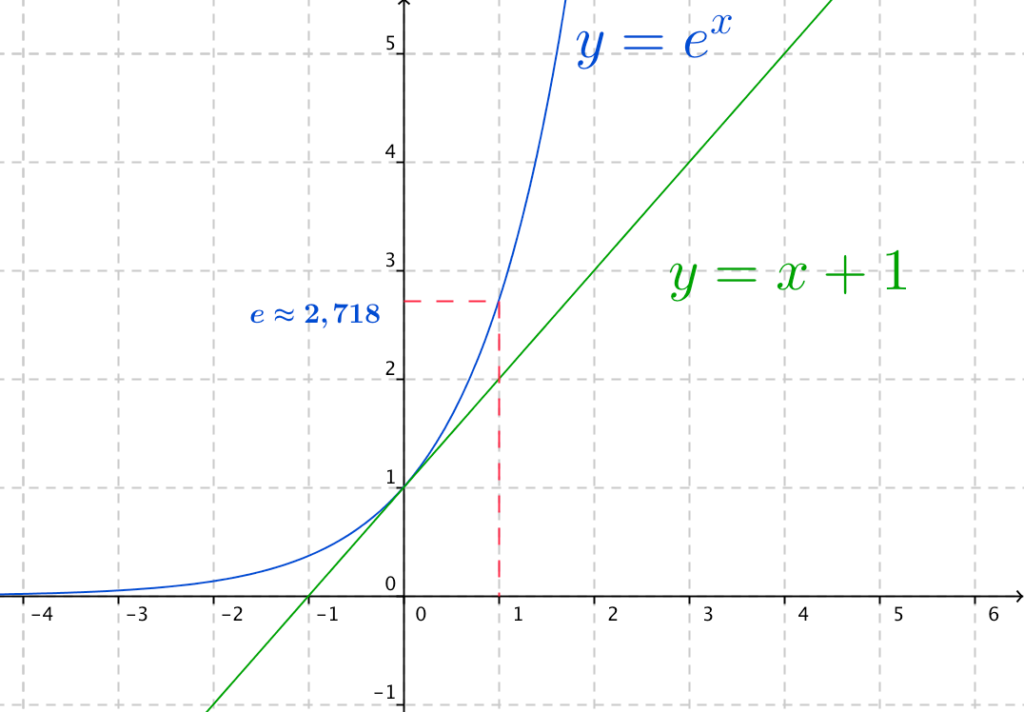
Représentation graphique de la fonction_exponentielle:

4- Dérivée de la fonction exponentielle x ↦ exp(u(x))

Soit u une fonction dérivable sur un intervalle I. Soit f la fonction définie sur I par :

Pour tout réel x de I, f(x) = exp(u(x)).

La fonction f est dérivable sur I et pour tout réel x de I, f′(x) = u′(x)exp (u(x)).

Exercice:

Soit f la fonction définie sur R par : Pour tout réel x, f(x) = xexp(−x²).

Déterminer la dérivée de f.

Solution :

Pour tout réel x, posons u(x) = −x² puis g(x) = exp(−x²) = exp(u(x)). La fonction u est dérivable sur R. Donc, la fonction g est dérivable sur R et pour tout réel x,

g′(x) = u′(x)exp(u(x)) = −2xexp(−x²).

On en déduit que f est dérivable sur R en tant que produit de fonctions dérivables sur R et pour tout réel x,

f′(x) = 1 × exp(−x²) + x × (−2xexp(−x²)) = exp(−x²) − 2x²exp(−x²) = (1 − 2x²)exp(−x²)

5- Primitives de la fonction exponentielle

1- Les primitives sur R de la fonction x ↦ exp(x) sont les fonctions de la forme x ↦ exp(x) + k où k est un réel.

2- Plus généralement, soit u une fonction dérivable sur un intervalle I. Les primitives sur R de la fonction x ↦ u′(x)eu(x) sont les fonctions de la forme x ↦ eu(x) + k où k est un réel.

En particulier, si a est un réel non nul et b est un réel, les primitives sur R de la fonction x ↦ exp(ax+b) sont les fonctions de la forme x ↦ 1/a exp(ax+b) + k où k est un réel.